Сумма векторов в линейной алгебре вычисляется покоординатно. Каждая координата результирующего вектора равна сумме соответствующих координат исходных векторов.
Содержание
Сумма векторов в линейной алгебре вычисляется покоординатно. Каждая координата результирующего вектора равна сумме соответствующих координат исходных векторов.
Основной принцип сложения векторов
Для двух векторов в n-мерном пространстве:
| Векторы | Координаты суммы |
| a = (a₁, a₂, ..., aₙ) | (a₁+b₁, a₂+b₂, ..., aₙ+bₙ) |
| b = (b₁, b₂, ..., bₙ) |
Примеры в различных пространствах
1. Двумерное пространство (R²)
- a = (x₁, y₁)
- b = (x₂, y₂)
- a + b = (x₁ + x₂, y₁ + y₂)
2. Трехмерное пространство (R³)
| Вектор a | Вектор b | Сумма a + b |
| (1, 2, 3) | (4, 5, 6) | (5, 7, 9) |
| (-2, 0, 4) | (3, -1, 2) | (1, -1, 6) |
3. N-мерное пространство (Rⁿ)
- Определить размерность пространства n
- Для каждой координаты i от 1 до n
- Вычислить сумму cᵢ = aᵢ + bᵢ
- Результат: (c₁, c₂, ..., cₙ)
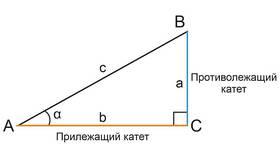
Геометрическая интерпретация
Покоординатное сложение соответствует:
- Правилу параллелограмма для двумерных векторов
- Последовательному отложению векторов в пространстве
- Диагонали параллелепипеда для трех и более измерений
Свойства покоординатного сложения
| Свойство | Описание |
| Коммутативность | a + b = b + a |
| Ассоциативность | (a + b) + c = a + (b + c) |
| Нейтральный элемент | a + 0 = a, где 0 - нулевой вектор |
Таким образом, каждая координата суммы векторов вычисляется независимо от других координат как сумма соответствующих координат слагаемых векторов.
